在数学领域，中点专题是一个重要且有趣的领域，它涉及到几何、代数、拓扑等多个方面，对于培养学生的空间想象能力和问题解决能力具有重要作用，本文将介绍中点专题的五大模型，帮助读者更好地理解和掌握这一专题。

平行四边形对角线中点模型

平行四边形对角线中点模型是中点专题中最基础、最重要的模型之一，在该模型中，平行四边形的对角线交于一点，该点是对角线的中点，此模型在证明线段平行、线段相等、面积关系等问题中具有广泛的应用。

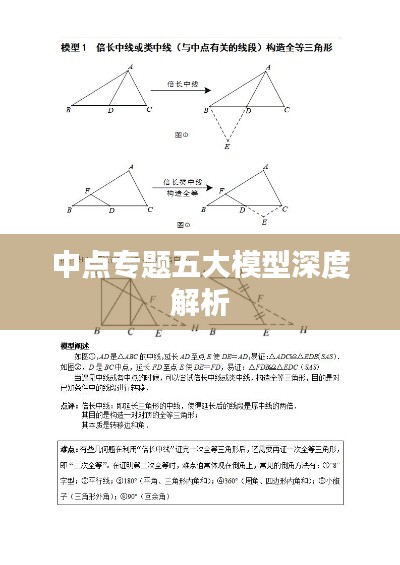
三角形中位线模型

三角形中位线模型是中点专题中另一个重要模型，在三角形中，连接顶点与其对边中点的线段称为中位线，该模型在证明线段比例、三角形面积等问题中具有重要作用，三角形中位线模型还可以与平行四边形对角线中点模型相互转化，为解决问题提供更多思路。

梯形中点模型

梯形中点模型涉及梯形两腰中点连线与两底之间的关系，该模型在证明线段平行、线段比例等问题中具有广泛应用，梯形中点模型还可以与三角形中位线模型相结合，为解决复杂问题提供便利。

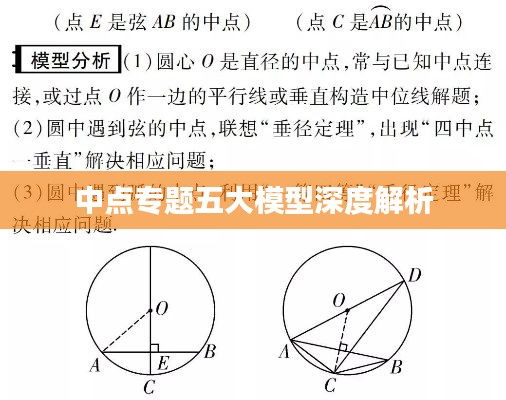
平行四边形性质及中点四边形模型

在平行四边形中，通过对角线连接各边的中点，可以得到一个中点四边形，该四边形一般为平行四边形，且其对角线与原平行四边形的对角线有关，这一模型在证明线段关系、角度关系等问题中具有重要作用，通过对中点四边形的性质进行研究，可以进一步拓展中点专题的应用范围。

复杂图形中的中点问题模型

在实际问题中，可能会遇到更为复杂的图形，如多个三角形、四边形组合而成的图形，针对这类问题，需要灵活运用前面介绍的模型，通过添加辅助线、构造中位线等方法，将复杂问题转化为简单问题，这需要学生具备较高的空间想象能力和问题解决能力。

中点专题的五大模型包括平行四边形对角线中点模型、三角形中位线模型、梯形中点模型、平行四边形性质及中点四边形模型以及复杂图形中的中点问题模型，这些模型在中点专题中具有重要的应用价值，对于解决线段关系、角度关系、面积计算等问题具有关键作用。

为了深入理解和掌握这些模型，我们需要多做练习，通过实践来加深对概念的理解，我们还需要善于总结和思考，找到不同模型之间的内在联系，以便更好地运用这些模型解决实际问题，希望通过本文的介绍，读者能够对中点专题的五大模型有更深入的了解。