在平面几何学中，圆与直线的交点问题是一个重要的研究领域，圆的切线作为与圆相交的一种特殊直线，其性质独特且应用广泛，本文将围绕“专题圆的切线”展开讨论，深入解析其定义、性质以及实际应用。

圆的切线的定义

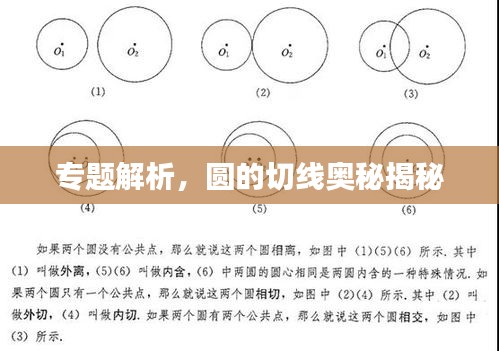
圆的切线是一种特殊的直线，它与圆的交点是唯一的，或者说没有交点，这种特性使得圆的切线在几何学中占据重要地位，当我们说一条直线是圆的切线时，我们意味着这条直线在某一特定点处与圆只有一个公共点。

圆的切线的性质

1、切线与半径垂直：这是圆的最基本的性质之一，一条通过圆心并且与切线相交的线（即半径）会与切线在交点处形成直角，这一性质在证明许多其他关于圆的切线性质时非常关键。

2、切线长度与半径的关系：对于给定的圆，其任意一条切线与半径的长度相等，这是基于切线与半径垂直的性质以及勾股定理推导出来的，这一性质在解决涉及切线的问题时非常有用。

3、切线的判定定理：如果一个直线经过圆上某一点，并且该直线在该点处的法线与该圆心的连线垂直，那么这条直线就是该圆的切线，这一判定定理为我们提供了一种判断直线是否为切线的方法。

圆的切线的应用

圆的切线的应用广泛，涉及到许多领域，以下是一些常见的应用：

1、几何学证明：在证明几何问题时，我们经常需要利用圆的切线的性质来证明一些结论，利用切线与半径垂直的性质来证明两条线段的长度相等。

2、物理学：在物理学中，许多运动轨迹可以近似为圆形路径，研究圆的切线可以帮助我们理解物体在圆形路径上的运动情况，研究物体在圆周上的滑动情况就需要用到圆的切线的知识。

3、工程学：在工程学中，许多机械部件的转动部分可以看作是在圆上移动，了解圆的切线的性质可以帮助工程师设计更高效的机械部件，轴承的设计就需要考虑到切线的性质，以确保轴承的平稳转动。

4、数学和物理学的教学：在教学领域，讲解圆的切线的性质和应用有助于学生更好地理解几何学和物理学的知识，通过解决涉及切线的问题，教师可以帮助学生巩固知识并提高他们的解决问题的能力。

本文详细讨论了“专题圆的切线”的相关知识，首先定义了圆的切线，然后介绍了其主要的性质，包括切线与半径垂直、切线长度与半径的关系以及切线的判定定理，本文还讨论了圆的切线的应用，包括在几何学证明、物理学、工程学和教学中的应用，希望本文能帮助读者更好地理解圆的切线的相关知识并能在实际中运用这些知识。